Putter Torque and Face Rotation

Introduction

Dr. Sasho MacKenzie’s research shows that successful putting requires managing three factors:

1. Start line
   • Primarily determined by face angle at impact
   • Tolerance: ±0.7° on 12-foot putts¹
2. Speed control
   • Determines capture width and is especially critical on breaking putts
   • Visual strategy (near vs. far focus) can affect speed control². This is the basis of “heads up” putting.
3. Aim/alignment
   • Where you point the putter at address
   • Many golfers consistently mis-aim by several degrees
   • Perfect face control can appear bad when it’s really an alignment issue. And vice versa.

Interestingly, path and contact location have much larger error tolerances - you’d need path errors of ±3.5° or contact errors of ±11mm to miss a 12-footer (far more forgiving than the ±0.7° face angle tolerance).¹ The main point is that putting performance depends on the interaction of these factors. Even perfect face control won’t overcome poor speed or mis-alignment.

This post focuses specifically on face contol and how putter design influences the torque acting to twist the face during the stroke.

---

Model

The Stroke Arc

Even in a perfectly on-plane putting stroke, the putter head does not move straight back and straight through. This is because the putter sits on an inclined plane determined by the lie angle, the head traces a circle in that tilted plane. When you look down from above, that circle appears as an ellipse on the green.

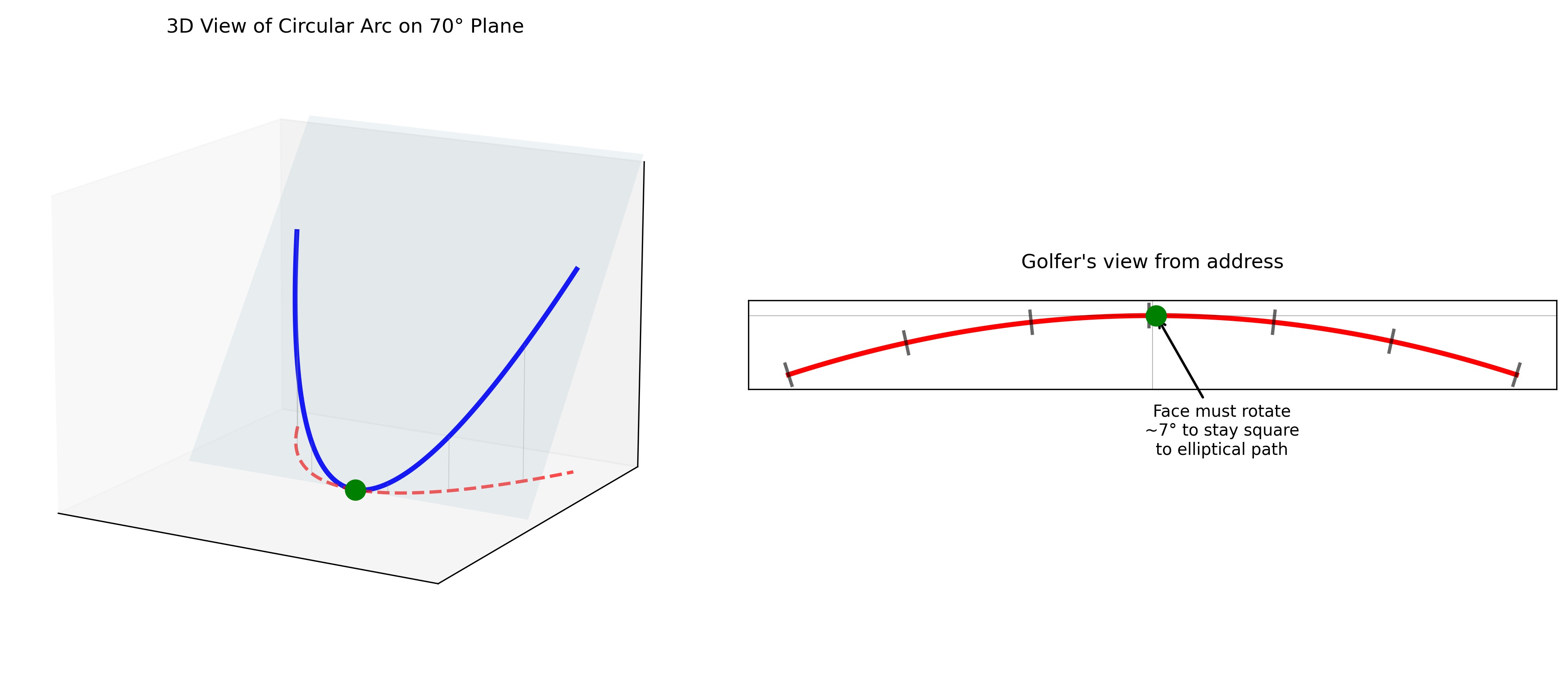
To keep the putter face square to the path, the face must rotate to remain perpendicular to the tangent of that ellipse. The needed face rotation is a purely geometric consequence of the lie angle.

Let:

• \(\phi\) = lie angle (typ. 68–72°)
• \(\theta\) = stroke angle within the tilted plane
• \(R\) = effective radius of the stroke arc

A convenient orthonormal basis for the tilted plane is:

\[\mathbf{e}_1 = (1,0,0), \qquad \mathbf{e}_2 = (0,\cos\phi,-\sin\phi)\]

Then the putter head’s position is:

\[\mathbf{r}(\theta) = R\cos\theta\,\mathbf{e}_1 + R\sin\theta\,\mathbf{e}_2 = \begin{pmatrix} R\cos\theta \\ R\sin\theta\cos\phi \\ -R\sin\theta\sin\phi \end{pmatrix}\]

Tangent

The tangent vector is:

\[\mathbf{t}(\theta) = \frac{d\mathbf{r}}{d\theta} = \begin{pmatrix} -R\sin\theta \\ R\cos\theta\cos\phi \\ -R\cos\theta\sin\phi \end{pmatrix}\]

Putting is judged in the horizontal plane, so we project the tangent into the \(x{-}y\) plane:

\[\mathbf{t}_{xy}(\theta) = \begin{pmatrix} -R\sin\theta \\ R\cos\theta\cos\phi \end{pmatrix}\]

The direction of the path on the green is the angle of this tangent:

\[\psi(\theta) = \arctan\left( \frac{R\cos\theta\cos\phi}{-R\sin\theta} \right) = \arctan\left( -\cot\theta \cdot \cos\phi \right)\]

This angle \(\psi(\theta)\) is exactly the orientation that the face must match to remain square to the arc.

Rotation

Near the center of the stroke (\(\theta = 0\)), a Taylor expansion gives:

\[\psi(\theta) \approx \theta\,\cos\phi\]

(small-\(\theta\) approximation)

This approximation is surprisingly good up to ±15–20°.

For a typical lie angle \(\phi = 70°\):

\[\cos\phi \approx 0.34\]

So for a modest stroke of ±20°:

\[\Delta\psi \approx 20° \times 0.34 \approx 6.8°\]

Interpretation

Even in a perfectly on-plane, mechanically ideal stroke:

• the putter face must open ~6–7° on the backswing, and
• must close the same amount on the follow-through

to stay square to the arc.

This arc is not a flaw. It is the natural outcome of swinging a putter on an inclined plane.

The design question becomes: does your putter fight this natural rotation or cooperate with it?

---

Torque Components

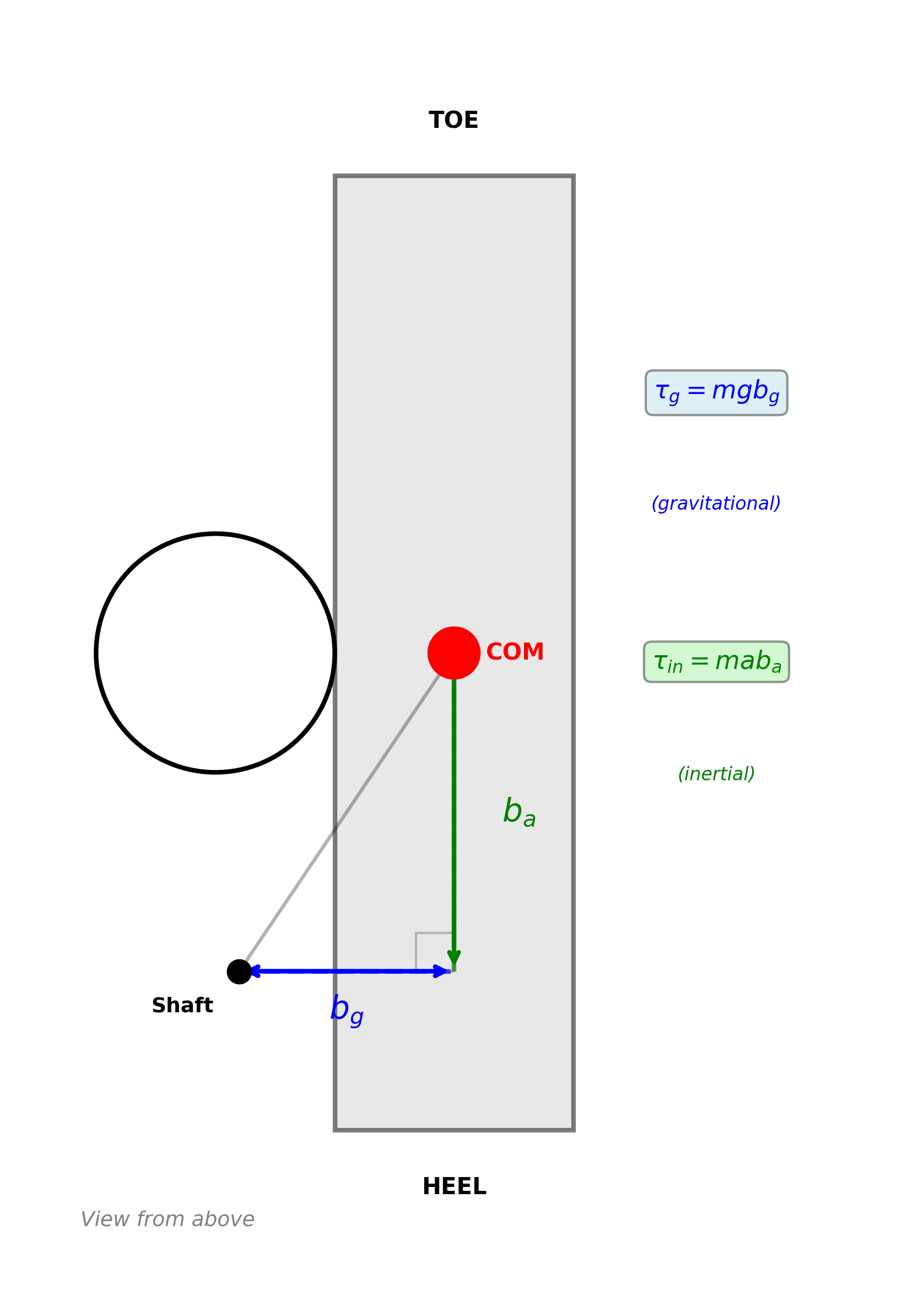
Two perpendicular COM offsets create torque about the shaft:

The total force acting on the putter head is:

\[\mathbf{F} = m\mathbf{a} + m\mathbf{g}\]

where \(m\) is the head mass, \(\mathbf{a}\) is the translational acceleration, and \(\mathbf{g}\) is gravity. This creates two independent torque contributions about the shaft:

1. Gravitational torque

\[\tau_g = m g b_g\]

This term is present even when the putter is held still. It depends on the front/back offset \(b_g\) — how far the COM “hangs” away from the shaft line.

• Positive \(b_g\) (forward) = face opens
• Negative \(b_g\) (onset) = face closes
• Always present, constant throughout stroke

2. Inertial torque

\[\tau_{in} = m a b_a\]

This term depends on how hard you accelerate the putter. It depends on the heel/toe offset \(b_a\) — the perpendicular distance from the acceleration force line to the shaft.

• Positive \(b_a\) (toe bias) = face opens during backswing
• Negative \(b_a\) (heel bias) = face closes during backswing
• Scales with acceleration, reverses on forward swing

Total torque and angular acceleration:

\[\alpha = \frac{\tau_s}{I_s} = \frac{\tau_{in} + \tau_g}{I_s}\]

where \(I_s\) is the moment of inertia about the shaft axis.

The key insight: \(b_g\) and \(b_a\) are independent geometric parameters. Different putter designs have radically different ratios, leading to very different torque profiles during the stroke.

---

Lie Angle Balance

A putter is lie-angle balanced when the shaft axis passes almost exactly through the putter head’s 3D center of mass (COM) when held at the actual lie angle. In that orientation:

• the gravitational force acts almost directly through the shaft, and
• the inertial force from accelerating the putter also acts almost through the shaft

so both produce near-zero torque about the shaft.

Torque about the shaft is:

\[\tau_s = (\mathbf{r}_{COM} \times \mathbf{F}) \cdot \hat{\mathbf{s}}\]

and lie-angle balance essentially makes \(\mathbf{r}_{COM} \approx 0\) in the relevant plane. This leads to a neutral feel where the putter does not want to open or close on its own during the stroke.

---

Estimates

Methodology

I focus on the first 50ms (1/20th second) of the backswing when acceleration begins and initial forces (potentially) try to rotate the face.

Why analyze only the initial 50ms? This “initial conditions” approach isolates what the putter naturally wants to do before compensatory hand forces take over. A full dynamic analysis of the putting stroke would require modeling the golfer’s counter-torques throughout the stroke. Without these, the putter would simply oscillate to a gravitational equilibrium with the COM hanging below the pivot point of the shaft. This doesn’t teach us anything about actual putting mechanics. By examining this initial impulse, we identify what forces the golfer must immediately counter with - revealing each design’s inherent tendency at stroke initiation. We can easily use the same approach, but in reverse, for the start of the downswing.

The analysis uses an impulse-based approximation:

Given torque and MOI, find rotation:

\[\tau = I_s \alpha \quad \Rightarrow \quad \alpha = \frac{\tau}{I_s}\]

For constant acceleration over time \(\Delta t\):

\[\Delta \theta = \frac{1}{2} \alpha (\Delta t)^2\]

The total torque is the sum of gravitational and inertial components:

\[\tau_{total} = \tau_g + \tau_{in} = m g b_g + m a b_a\]

Parameters:

• Head mass: \(m = 350\) g
• Gravity: \(g = 9.8\) m/s²
• Acceleration range: \(a = 6\)–\(12\) m/s² (smooth to aggressive backswing)
• Impulse duration: \(\Delta t = 50\) ms

For each putter design, we calculate the face rotation during this critical window using the geometry (\(b_g\), \(b_a\)) and resistance to rotation (\(I_s\)).

Results

Design	\(b_g\)	\(b_a\)	\(I_s\)	Torque	Rotation (50ms)	Character
Toe-Hang Blade	+19 mm	-51 mm	12,000 g·cm²	0.04–0.15 ft-lb	-2.5° to -8.8° (closes)	Inertial dominates 2-3×, fights arc
Face-Balanced Mallet	+51 mm	-1 mm	11,000 g·cm²	0.17–0.18 ft-lb	+11.3° to +11.1° (opens)	Gravitational dominates 50-80×, largest torque
L.A.B.	-1 mm	+1 mm	2,500 g·cm²	0.001–0.006 ft-lb	-0.4° to +0.2° (neutral)	Torques cancel, 50× smaller than face-balanced
Auto-Correcting	0 mm	+2 mm	2,500 g·cm²	0.003–0.006 ft-lb	+1.2° to +2.4° (opens)	Purely inertial, gentle arc assist

Note that values for \(b_a\) and \(b_g\) are representative. In particular, for the LAB example, I intentionally added a small tolerance that seems reasonable to assume as manufacturing tolerance. In this sense, we can read the LAB numbers as a worst case scenario.

Key observations:

• Face-balanced putters, surprisingly, have the largest torque, creating an immediate +11° opening bias
• Toe-hang putters close the face -2.5° to -8.8°, fighting the required ~7° opening for arc geometry
• L.A.B. putters achieve near-zero rotation (±0.3°) by using opposite-signed offsets that cancel
• Auto-correcting putters gently assist the natural arc with +1.2° to +2.4° opening

---

Implication

Face angle tolerance is ±0.7° on a 12-footer. The first 50ms of the backswing sets up the entire stroke:

• Face-balanced: Opens +11° immediately - you must fight this throughout the stroke
• Toe-hang: Closes -2.5° to -8.8° - fighting the natural 7° arc requirement
• L.A.B.: ±0.3° - essentially neutral, you control everything
• Auto-correcting: +1.2° to +2.4° - gently assists the required 7° opening

On the forward swing, the inertial torque reverses direction (acceleration flips sign), while gravitational torque remains constant:

• Face-balanced: Still opens (+11°) - constant gravitational bias in both directions
• Toe-hang: Now opens (reversal) - inertial torque flips, potentially helping close the required 7°
• L.A.B.: Still neutral (±0.3°) - torques still cancel
• Auto-correcting: Now closes (reversal) - gently assists the required 7° closing to square the face

The torque magnitude matters less than whether it helps or fights your natural stroke mechanics at each phase.

---

MOI

Higher MOI (\(I_s\)) reduces angular acceleration for the same torque:

\[\alpha = \frac{\tau}{I_s}\]

Implications:

• Resists unexpected twitches or “jerky” strokes.
• Requires more force to actually counteract the natural torques described above.

This is why high-MOI face-balanced mallets can feel “sticky”. The large gravitational torque tries to open the face, but large MOI makes it harder to resist that rotation.

---

Comparison

Design	Torque Magnitude	Initial Rotation (50ms)	Character
Face-Balanced	0.17-0.18 ft-lb	+11° (opens)	Constant bias, largest torque
Toe-Hang	0.04-0.15 ft-lb	-2.5° to -8.8° (closes)	Fighting arc, acceleration-dependent
L.A.B.	0.001-0.006 ft-lb	±0.3° (neutral)	Minimal, near-zero
Auto-Correcting	0.003-0.006 ft-lb	+1.2° to +2.4° (opens)	Gentle arc assist, scales with acceleration

---

Summary

Stroke geometry: Even in a perfect on-plane stroke, the face must rotate ~7° (open during backswing, close during forward swing) to stay square to the elliptical path created by the lie angle. This is the “neutral” path.

Torque sources: The location where the shaft points relative to the Center of Mass (COM) can create independent torques:

• Gravitational: \(\tau_g = mgb_g\)
• Inertial: \(\tau_{in} = mab_a\) (scales with acceleration, reverses on forward swing)

Peak Acceleration: I analyze the first 50ms of the backswing, when acceleration peaks, to estimate the behavior of these different designs when first put in motion. In reality, modeling the full dynamic system requires recognizing that the values \(b_a\) and \(b_g\) change as the face rotates, which requires that we assume counter-torque values that the hands must apply. What we care about in this analyis is only what initial forces the hands must apply to keep the putter face square when you start your putting stroke. It is straighforward to extend this to the moment of transition from the backswing to the downswing .

Design comparisons:

• Face-balanced: Largest magnitude rotation under our assumptions, opening +11° immediately. This is driven by constant gravitational bias you must fight throughout the stroke, including on the downswing, when the putter will still want to open.
• Toe-hang: Closes -2.5° to -8.8° on backswing, should open about the same amount at the start of the downswing. Possible that with some of the larger toe-hang mallets, gravitational torque and inertial torque get close to canceling each other out? Larger gravitational torque balances with a similarly large (and opposite) inertial torque? Maybe work for a future post.
• L.A.B.: Near-zero torque even if we assume the worst with manufacturing tolerance (±0.3°).
• Auto-correcting: Gently assists arc geometry (+1.2° to +2.4° opening on backswing, reverses to help close on forward swing). My personal favorite idea wise.

For your golf:

1. Have fun and pick a putter that makes you enjoy putting.
2. If you identify that you’re struggling to hit your line consistently, realize it’s most likely a face control problem, not a path problem.
3. Try a “zero-torque” putter with a few caveats:
   • You still need to aim it well. The onset can take some getting used to.
   • When you putt, you may need to resist the urge to “help” keep the face square.
   • Make a practice stroke without a golf club: this is the right mental approach as you really only have to focus on distance now, and not rotation.
4. If that doesn’t work for you, try a toe-hang mallet. In this case, two wrongs might actually make a right?